时间复杂度

1. 初始化向量p、f和g，时间复杂度为O(n)。
2. 第一个循环是素数筛法，它的时间复杂度是O(n log log n)。该循环遍历了从2到根号n的每个数i，如果p[i]为true，则将i的所有倍数p[j]（j >= i）标记为false。同时，还计算了f[j]和g[j]的值。
   • 外层循环的迭代次数是根号n，时间复杂度为O(sqrt(n))。
   • 内层循环的迭代次数是log n的级别，因为每次迭代i都会乘以i。时间复杂度为O(log n)。
   • 在内层循环中，还进行了一些常数时间的操作，如向向量d添加元素、反转向量d、以及标记p[j]、f[j]和g[j]的值。这些操作的时间复杂度可以忽略不计（O(1)）。
     如果vector使用insert()插入，时间复杂度为O(n)。类似的还有：erase()。而set（红黑树）实现的插入和擦除，时间复杂度为O(log n)。

for (int i = 2; i * i <= n; i++) {
	if (p[i]) {
		vector<int> d;
		for (int k = i; k <= n; k *= i)
			d.push_back(k);
		reverse(d.begin(), d.end());
		for (int k : d) {
			for (int j = k; j <= n; j += k) {
				if (p[j]) {
					p[j] = false;
					f[j] = i;
					g[j] = k;
				}
			}
		}
	}
}

2. 第二个循环是将剩余的素数添加到f和g中，时间复杂度为O(n)。
   • 外层循环的迭代次数是n - sqrt(n)，时间复杂度为O(n)。
   • 在内层循环中，只进行了一些常数时间的操作，如标记f[i]和g[i]的值。这些操作的时间复杂度可以忽略不计。

for (int i = sqrt(n) + 1; i <= n; i++) {
	if (p[i]) {
		f[i] = i;
		g[i] = i;
	}
}

3. 第三个循环是计算f的值并求和，时间复杂度为O(n)。
   • 循环的迭代次数是n - 1，时间复杂度为O(n)。
   • 在每次迭代中，我们进行了一些常数时间的操作，如计算f[i]的值和更新sum的值。这些操作的时间复杂度可以忽略不计。

for (int i = 2; i <= n; i++) {
	f[i] = f[i / g[i]] * (g[i] * f[i] - 1) / (f[i] - 1);
	sum += f[i];
}

solve1()函数的时间复杂度为O(n log log n) + O(n) + O(n) + O(n) = O(n log log n)。

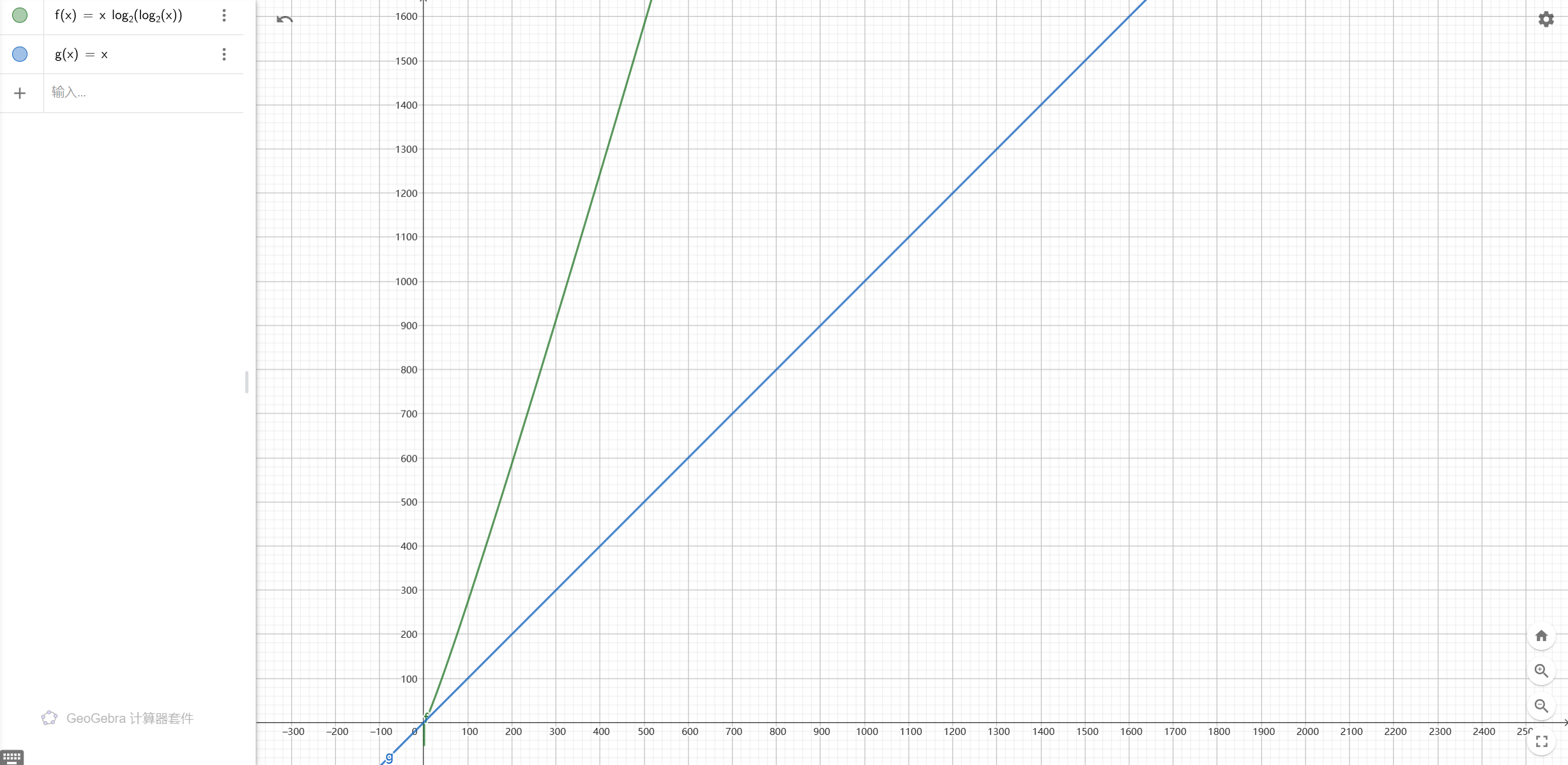
时间复杂度比较

solve1()和solve2()时间复杂度随输入值的变化图像：

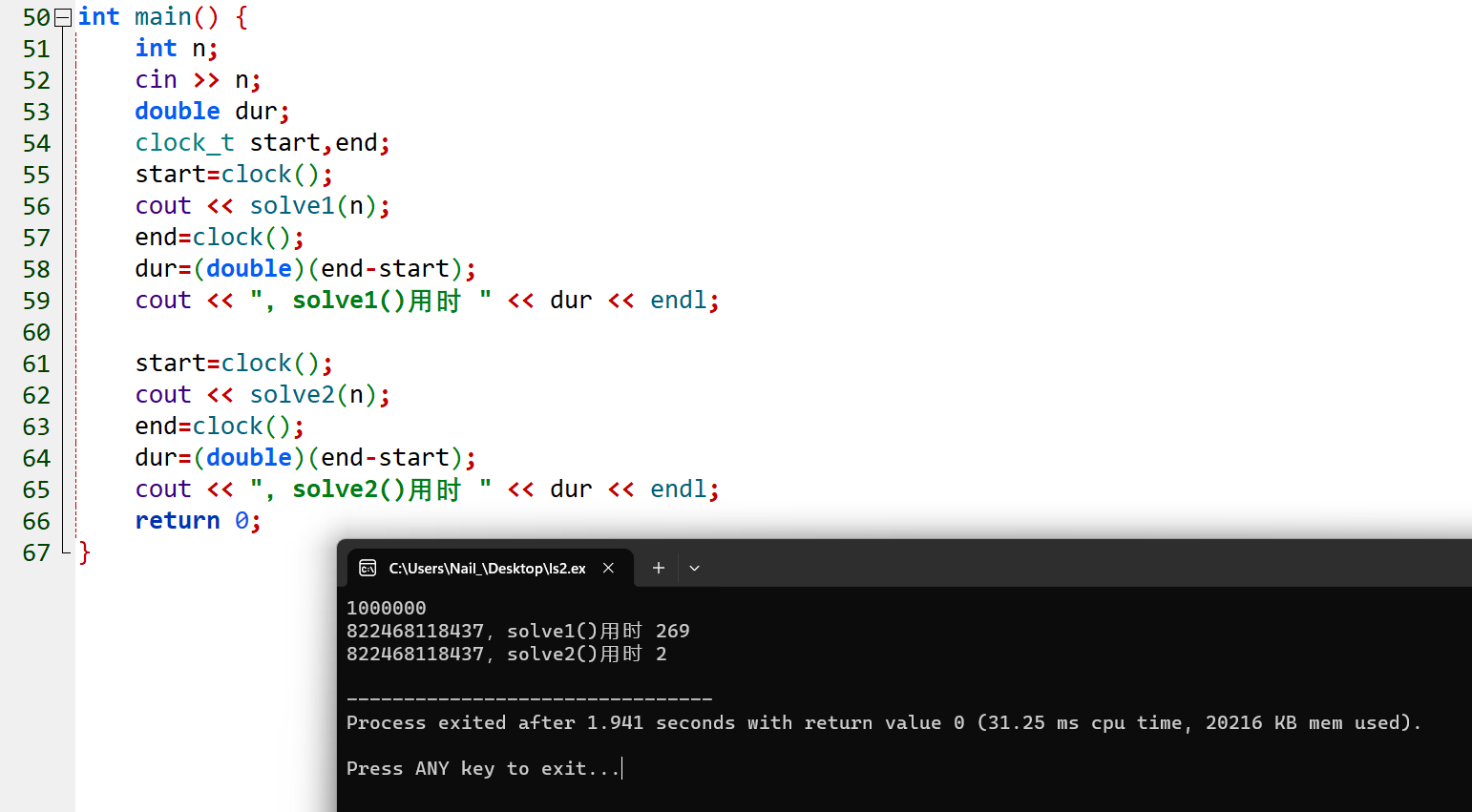
两函数运算大数据用时对比：

函数作用

solve1()函数中的变量p是一个布尔型vector，用于标记该数是否算了f和g。变量f和g是两个（长）整型vector，f：每一位存储该位置值的最小素因数，j（在执行第3个循环之前）：每一位存储该位置值的最小素因数的（最小素因数个数）次方。如下文图。难点：f和j的作用和值（f在第3个循环执行前后的两种值）。

在函数的第一个循环中，使用了素数筛法的思想：通过遍历从2到根号n的最小素数i，遍历$j=i^{pow}$到$i^1$($i^{pow} \le n$)，把没有算过的j计算f和j，强调计算f和j的顺序（2点，题目考了翻转的作用）。

第二个循环之前，f和g中小于等于sqrt(n)的位置已填完，大于的位置合数已填完，素数仍为初始化的0。第二个循环将剩余的素数计算f和g（即本身）。

第三个循环用了递推思想，先更改了f的值，再累加计算sum。最难的一处（未考）：

涉及到了欧拉函数（Euler's Totient Function）。这个函数通常表示为 $\phi(n)$，它是小于或等于n的正整数中与n互质的数的个数。

欧拉函数具有以下性质：

1. 素数的欧拉函数值：对于素数p，其欧拉函数值为$\phi(p) = p - 1$。这是因为素数与除了自身以外的所有数都是互质的。

2. 欧拉函数的乘性性质：如果a和b互质（即它们的最大公约数为 1），那么$\phi(ab) = \phi(a) * \phi(b)$。这个性质可以用来简化欧拉函数的计算。

3. 递推公式：对于正整数n和其最小素因数p，可以使用递推公式来计算欧拉函数值：
   $\phi(n) = \phi(n / p) * (p - 1)$，其中p是n的最小素因数。

在该循环中，利用了这个递推公式来计算每个数的欧拉函数值，从而得到所有数的欧拉函数值的和。这个函数通过素因数分解来获取每个数的最小素因数和其幂次，利用欧拉函数的性质递推地计算出每个数的欧拉函数值，并将这些值累加得到最终的数之和。

for (int i = 2; i <= n; i++) {
	f[i] = f[i / g[i]] * (g[i] * f[i] - 1) / (f[i] - 1);
	sum += f[i];
}

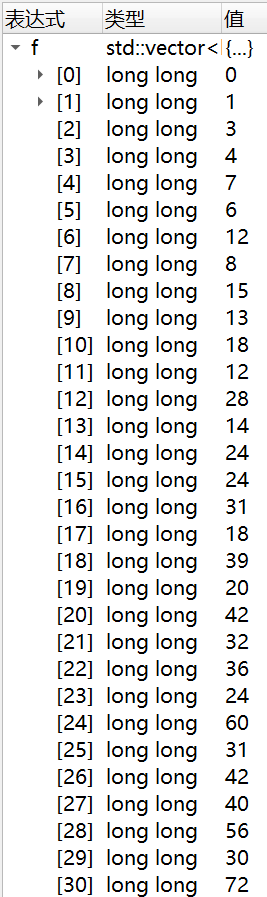
如位数i为24（原f[24]为2，g[24]为8）：

f[24]=f[24/g[24]] * (g[24]*f[24] -1) / (f[24]-1)

f[24]=f[24/8] * (8*2 -1) / (2-1)

f[24]=f[3] * 15 / 1，其中f[3]==4

f[24]=4 * 15 / 1，因此f[24]被重新赋值为60。

$24=2\times 2 \times 2 \times 3 = 2^3 \times 3=g[i]\times (i/g[i])$ 。

---

其实solve1()和solve2()的作用是相同的，两个函数的作用可参考solve2()：

long long solve2(int n) {
	long long sum = 0;
	for (int i = 1; i <= n; i++) {
		sum += i * (n / i);
	}
	return sum;
}

用公式表示，solve1()和solve2()求的都是：$\large \sum_{i=1}^{n} (i \times \lfloor n \div i \rfloor)$ 。

以输入5为例：

$\begin{aligned} sum &= 1 \times 5/1 + 2 \times 5/2 + 3 \times 5/3 + 4 \times 5/4 + 5\times 5/5 \\ &= 1\times 5 + 2\times 2 + 3\times 1 + 4\times 1 + 5\times 1 \\ &= 5+4+3+4+5 \\ &= 21 \end{aligned}$

f和g容器存储的值

以输入30为例：

到第3个循环之前（图1、图2）和执行完第3个循环之后：

link

题目链接：洛谷

题目代码（含注释）：本站